The Teacher As Mathematician Guest Post by Ann Elise Record
Subtraction is the Achilles’ Heel of our Students: But it Doesn’t Need to Be
By Ann Elise Record
In my 20 years as an educator in the role of classroom teacher, Math Coach K-5, and currently independent math consultant, one of the observations I’ve had is that subtraction takes the students out! For the younger students, I witness them counting back on their fingers to determine a fact like 15 - 8. For the upper elementary students, I witness them doing the exact same thing except this fact is embedded with the subtraction algorithm within a division problem. In this post, I’d like to share with you some ways we can explore subtraction that will help students develop flexible strategies starting with basic facts and the future impact as they apply these same strategies to the numbers appropriate to their grade level. If we dedicate instructional time to subtraction (equal to the other operations), we can ensure access to the mathematics for all our students.
First of all, I want to be clear that students using their fingers to count back isn’t what bothers me. They are a “handy” manipulative that students always have with them and I never want any student to feel shame in using them. I would use my fingers, too, if I were counting back a large number like an 8. The issue is that the students are in the counting phase of reasoning. Here is graphic of the K-12 math journey made by Pam Harris of www.mathisfigureoutable.com that has profoundly affected my understanding of students’ mathematical development.
Subtraction Basic Facts
In Preschool and Kindergarten, students are in the world of counting and cardinality. There is a lot going on in these grade levels and we definitely expect them to use their fingers to explore quantities and begin to explore addition and subtraction. In grades 1 and 2, though, we want to explore quantities in ways that will help students develop their understanding of number relationships. Not only will we be helping students arrive at their answers more efficiently, but they will be developing their conceptual understanding of the operations as well as their number sense.. There are two keys to developing fluency with subtraction: decomposing numbers and realizing there are two meanings of subtraction.
Subtraction Fluency within 10
The first context we use when we explore subtraction with our youngest students involves the action of removing items so objects get eaten, broken, or given away. Because this action is in the story problem, it becomes natural that students act out the problem and count the objects as they remove them and then count the ones that are left. As our students are introduced to working with larger numbers in grades 1 and 2, we want to help them move past the counting phase of reasoning and into additive thinking. The first step on this journey is to explore the second meaning of subtraction: finding the distance between the two numbers. A context such as Kylynn has 8 cookies and Delia has 6. How many more cookies does Delia need to have the same as Kylynn? This story situation encourages using addition to solve subtraction. So, rather than counting back 6, we can start at the 6 and count up to the 8. This is a tell-tale expression I use when I interview students on their basic facts using Dr. Nicki Newton’s Math Running Records (www.mathrunningrecords.com). At the same time, we can be exploring the decomposition pairs of all the numbers up to 10 so that if I ask a student 8 - 6 they will know it is 2 because 6 + 2 = 8.
For me, the most powerful and versatile manipulative is CuisenaireⓇ Rods (The name Cuisenaire Rods and the color sequence of the rods are registered trademarks of hand2mind). Since they are not labeled with values, they can represent anything we wish - whole numbers, decimals, and fractions. Since the quantities exist as a group, we can help students focus on the number relationships and move beyond counting with addition and subtraction (and beyond skip counting with multiplication and division). Here is the color coding system of the rods…
They are a perfect manipulative to help students determine all the decomposition pairs of all the numbers up to 10. Here’s an example with the number 5.
Subtraction Fluency within 20
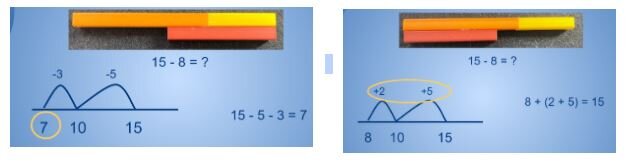
As we move into subtraction facts within 20, we want students to use strategies that make sense for their brains. Some prefer the removal thought process while others prefer to think addition. We never want to dictate which strategies students use, but we can show that some strategies are more efficient with certain numbers than others. This is particularly true with subtraction. Our choice of manipulatives can play a crucial role in developing our student’s efficiency. Rather than counting back or counting up, students can think in chunks using 10 as a bridge. Here are two examples using Cuisenaire rods and notice the difference in the thinking to arrive at the same difference of 7.
I was interviewing a 2nd grader recently using the Math Running Record and when I asked her 14 - 8, she counted up from the 8 to get up to the 14. Here’s a conversation we had together once the interview was done.
If you are interested in learning more about how you can explore the basic facts of addition and subtraction in concrete, pictorial, and abstract ways, check Dr. Nicki Newton, Dr. Alison Mello, and my book called Fluency Doesn’t Just Happen with Addition and Subtraction.
Future impact
The power of this work in the basic fact fluency is that those very same strategies can be used when students are working on the content standards of their grade level. Too often our students are getting caught in the counting phase of reasoning within their work with multi-digit numbers. Let’s take a moment to think about the thought processes of the students in a traditional algorithm to subtract 102 - 98. Students typically begin in the ones place and realize (not always!) that there aren’t enough in the ones place to remove 8. If they are able to successfully regroup across those zeros, they will need to think about 12 - 8. Too often at this point, students have not developed fluency yet and fall back to a comfortable place by counting back the 8 from 12. They then do the same thinking in the other place value positions. So essentially, students have only thought about basic facts and are even counting to determine the differences.
Yet, if they had explored their basic facts by using strategies such as using addition to solve subtraction, they could think about the distance between 98 and 102 which is much easier for their brains. By making the thinking visible within the work of basic facts using manipulatives, students are able to visualize the same thinking process within the context of multi-digit numbers and even decimals and fractions down the road. This is so very powerful! Here’s an example of how we can help students develop flexible strategies using Cuisenaire rods with 2-digit subtraction.
Finally, here’s a video of a conversation with a 3rd grader about subtraction after a Math Running Records interview. I had asked her 15 - 8 and she had said you can add two to get to 10, then add 5 to get to 15 so the difference was 7. Yet, when I asked her some subtraction problems which could become attainable with mental math using the adding up thought process, she didn’t use it.
There truly is nothing elementary about teaching elementary math. In fact, the more I learn, the more I realize I need to learn. Let’s work together to help students develop fluency. I’d love to hear from you either through Facebook, Twitter, or by email. Down below, I’ve included those links. If I’ve peaked your interest in Cuisenaire rods, I do have two on-demand workshops for K-2 and 3-5 in which I explore how we can use Cuisenaire rods for fluency, problem solving, and the content standards for every grade. You can find there at https://www.anneliserecord.com/courses-new.
Together we can provide access to all our students and will be creating students who are engaged, curious, flexible, risk-taking, and confident mathematicians!
Ann Elise Record is an elementary math specialist/consultant.
Website and newsletter signup: www.anneliserecord.com
Facebook: https://www.facebook.com/annelise.record.94
Twitter: @AnnEliseRecord
Instagram: ann.e.record
Email: aer@anneliserecord.com